Το Tracker είναι ένα λογισμικό ανοιχτού κώδικα, που χρησιμοποιείται για ανάλυση βίντεο και μοντελοποίηση και μπορεί να βρει εφαρμογές στη διδασκαλία των Φυσικών Επιστημών.
Μπορείτε να το κατεβάσετε από εδώ.
Στην ίδια ιστοσελίδα, και συγκεκριμένα σε αυτό το σύνδεσμο, μπορείτε να βρείτε οδηγίες εγκατάστασης και χρήσης στα ελληνικά.
Εδώ μπορείτε να βρείτε απλές οδηγίες για να αξιοποιήσετε τις βασικές δυνατότητες του προγράμματος, μέσω δύο παραδειγμάτων. Και στα δύο παραδείγματα βιντεοσκοπήσαμε το πείραμα και το εισάγαμε στο Tracker. Είναι σημαντικό να ξεκινήσουμε με καλής ποιότητας βίντεο, ώστε να γίνει πιο εύκολη η επεξεργασία του. Συγκεκριμένα, πρέπει να προσέξουμε:
- Η κάμερα να “στοχεύει” στο κέντρο της σκηνής που θέλουμε να καταγράψουμε και η λήψη να είναι κάθετη στο επίπεδο που εκτελείται το πείραμα, ώστε να υπάρχουν οι μικρότερες δυνατές παραμορφώσεις, λόγω γωνιών.
- Εφόσον θα καταγράψουμε την κίνηση κάποιου αντικειμένου, όσο πιο ευκρινές είναι αυτό στο βίντεο, τόσο πιο εύκολη θα γίνει η δουλειά μας αργότερα. Άρα, προσπαθούμε να έχουμε ένα αντικείμενο με έντονο, φωτεινό χρώμα και όσο το δυνατό ομοιόμορφο και μεγάλης αντίθεσης φόντο.
Α. Μελέτη απλής αρμονικής ταλάντωσης.
Το βίντεο που τραβήξαμε για το πείραμα αυτό μπορείτε να το κατεβάσετε από τον ακόλουθο σύνδεσμο, ώστε να το χρησιμοποιήσατε, αν θέλετε, για εξάσκηση.
Για να δούμε τις δυνατότητες του λογισμικού και για να πετύχουμε καλύτερη αποτύπωση των δεδομένων, χρησιμοποιήσαμε για κάμερα κινητό που επιτρέπει τη λήψη με 240 καρέ ανά δευτερόλεπτο (fps).
Έχοντας το βίντεο, ανοίγουμε την εφαρμογή Tracker και από το μενού επιλέγουμε το File -> Open File και εισάγουμε το βίντεο (εικόνα 1).
Εικόνα 1
Είναι πολύ πιθανό να μη θέλουμε να αξιοποιήσουμε ολόκληρο το βίντεο για το πείραμά μας. Μπορούμε να ορίσουμε το πρώτο και το τελευταίο καρέ του τμήματος που θεωρούμε χρήσιμο, ως εξής: Μετακινούμε την μπάρα κάτω από το βίντεο, είτε σέρνοντάς την, είτε με τα μπλε βέλη στο δεξιό άκρο της μπάρας, για μεγαλύτερη ακρίβεια. Όταν εντοπίσουμε το καρέ από το οποίο θέλουμε να ξεκινήσει η μελέτη, κάνουμε δεξί κλικ και επιλέγουμε “Set start frame to slider (X)”, όπου Χ ο αριθμός του καρέ που επιλέξαμε (εικόνα 2). Το ίδιο κάνουμε, αν χρειάζεται και για το τέλος του τμήματος που θέλουμε να μελετήσουμε.

Εικόνα 2
Το επόμενο βήμα είναι να ορίσουμε κάποιο πρότυπο μέγεθος μήκους. Επιλέγουμε το εικονίδιο που φαίνεται σε κόκκινο κύκλο στην εικόνα 3 και στη συνέχεια επιλέγουμε “Calibration Stick”. Για μεγαλύτερη ακρίβεια, χρησιμοποιήσαμε ως πρότυπο μήκους το νήμα που χρησιμοποιήσαμε για τη μελέτη της ταλάντωσης, το οποίο ήταν 60 cm. Κρατώντας πατημένο το “Shift” κάνουμε κλικ στην αρχή και το τέλος του νήματος και στη συνέχεια κάνουμε κλικ στην τιμή που εμφανίζεται και ορίζουμε το γνωστό μήκος (εικόνα 4).
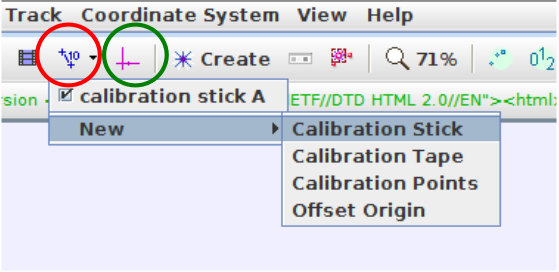
Εικόνα 3
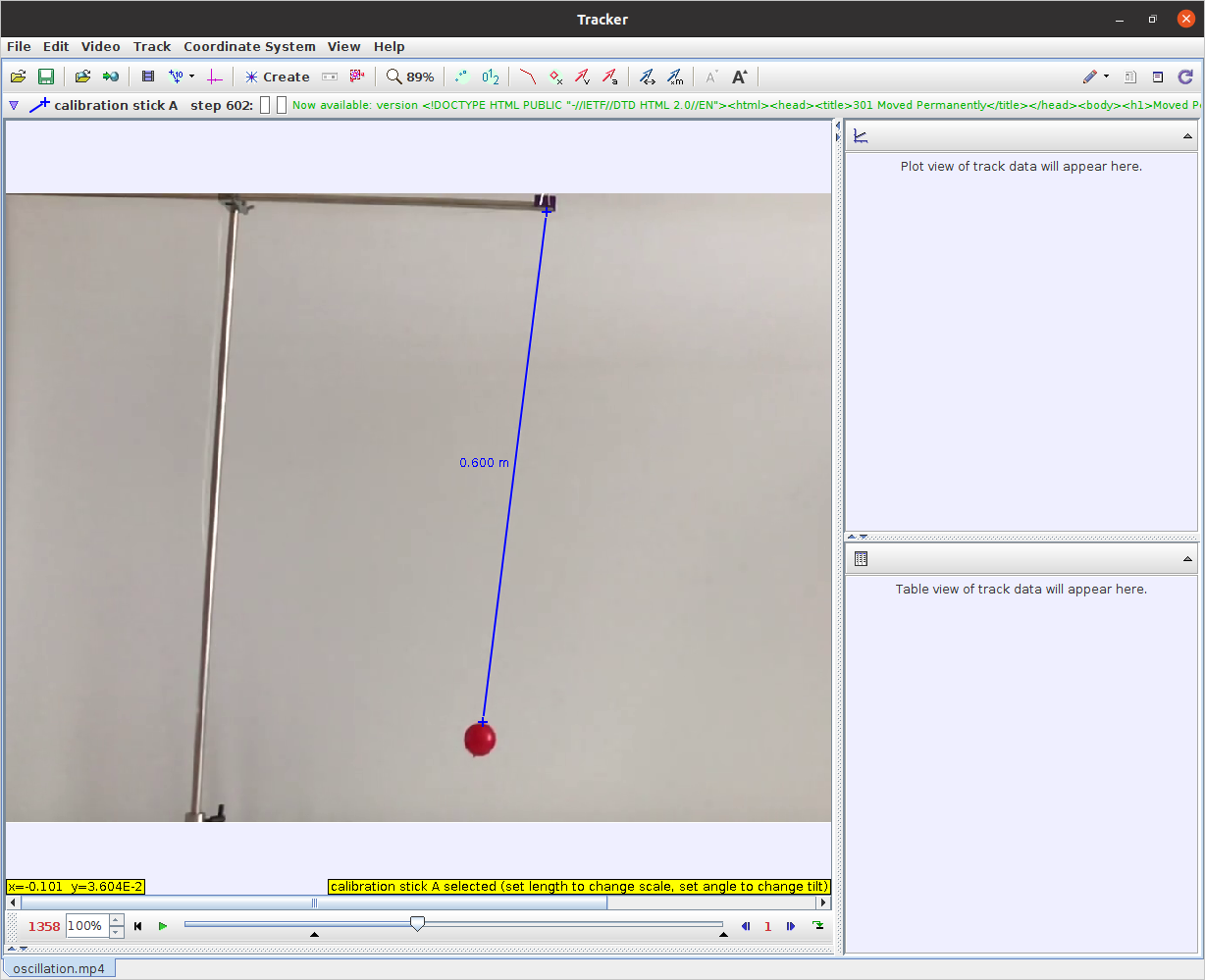
Εικόνα 4
Στη συνέχεια αν κάνουμε κλικ στο εικονίδιο που είναι σε πράσινο κύκλο στην εικόνα 3, εμφανίζεται το σύστημα αξόνων. Κάνοντας κλικ στο κέντρο των αξόνων μπορούμε να μεταφέρουμε την αρχή των αξόνων στο σημείο που επιθυμούμε (εικόνα 5). Εδώ να υπενθυμίσουμε ότι όσο πιο καλή κινηματογράφηση έγινε (να είναι οριζόντια η κάμερα, να τραβάει κάθετα τη σκηνή, κτλ) τόσο μικρότερη διόρθωση χρειάζονται οι άξονες. Αν χρειαστεί κάτι τέτοιο, μπορούμε να κάνουμε κλικ στο θετικό τμήμα του άξονα x και να περιστρέψουμε το σύστημα όσο χρειάζεται.
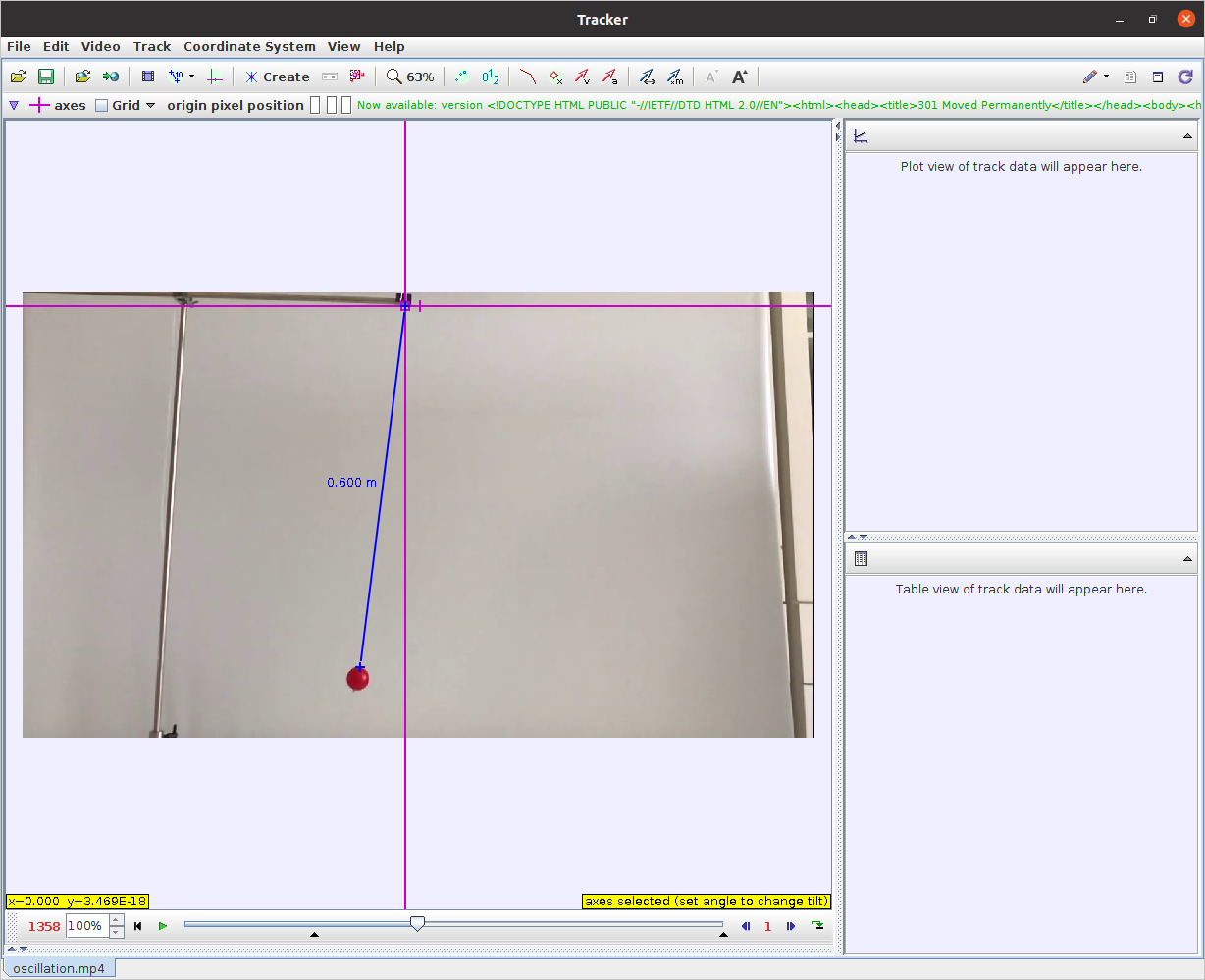
Εικόνα 5
Επόμενο βήμα, κάνουμε κλικ στο “Create” και επιλέγουμε “Point Mass” (εικόνα 6) και στη συνέχεια κλικ στο εικονίδιο ![]() , που είναι στα δεξιά του.
, που είναι στα δεξιά του.

Εικόνα 6
Εμφανίζεται ένα παράθυρο όπως αυτό της εικόνας 7.
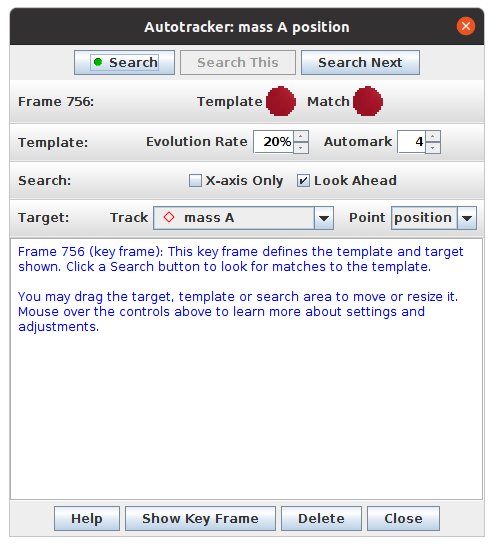
Εικόνα 7
Αυτή είναι η λειτουργία “Autotrack”, όπου ορίζουμε ένα πρότυπο σώμα στο αρχικό καρέ και ο υπολογιστής, ακολουθώντας το χρωματικό πρότυπο, προσπαθεί να το εντοπίσει στα υπόλοιπα. Το πρότυπο σώμα το επιλέγουμε κρατώντας τα “Shift” και “Ctrl” πατημένα και κάνοντας κλικ πάνω στο σώμα που επιθυμούμε. Στο σημείο που κάναμε κλικ εμφανίζεται ένας κύκλος και έξω από αυτόν ένα τετράγωνο (εικόνα 8). Ο κύκλος ορίζει τη χρωματική περιοχή πρότυπο, ενώ το τετράγωνο, το εύρος της επιφάνειας στην οποία ο υπολογιστής θα αναζητά αυτό το πρότυπο. Σέρνοντας το κάτω δεξί άκρο μπορούμε να αυξομειώσουμε το εμβαδό τους, ώστε να πετύχουμε autotracking με τις λιγότερες δυνατές αστοχίες. Πατώντας “Search” στο παράθυρο της εικόνας 7 ο υπολογιστής αναζητά το σώμα στα επόμενα καρέ. Αν υπάρξει κάποια αστοχία, σταματά η αναζήτηση. Σε αυτή την περίπτωση, στο προβληματικό καρέ ορίζουμε ξανά το σώμα, με “Shift” και “Ctrl” πατημένα και κάνοντας κλικ πάνω στο σώμα και συνεχίζουμε.

Εικόνα 8
Καθώς προχωράει η ανάλυση των καρέ, βλέπουμε να σχηματίζονται και οι γραφικές παραστάσεις (εικόνα 9, γραφική παράσταση x=f(t)). Μπορούμε να δούμε πολύ καθαρά τη μορφή της καμπύλης, αλλά και το ότι το πλάτος της ταλάντωσης μειώνεται ελαφρά με την πάροδο του χρόνου.
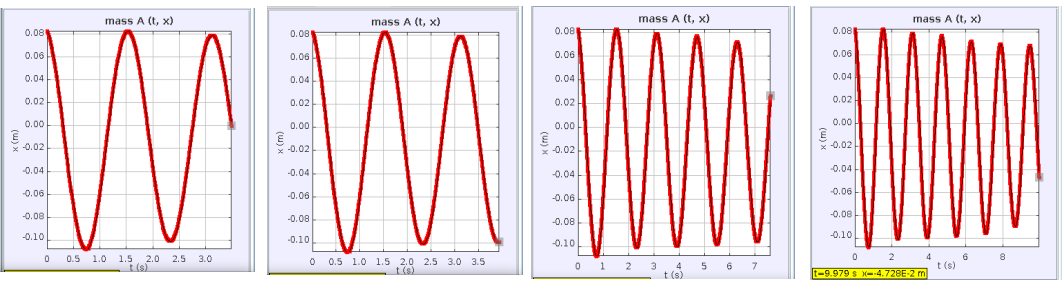
Εικόνα 9
Ένα παράδειγμα ποσοτικής εφαρμογής είναι ο υπολογισμός της περιόδου, μετρώντας τη χρονική απόσταση δύο μέγιστων στην καμπύλη.
Στο συγκεκριμένο παράδειγμα, προκύπτει ότι Τ=1,58 s.
Με βάση τη θεωρία,
, όπου, για l=0.6 m και g=9.81 m/s2, T=1.55 s.
Β. Μελέτη κύλισης κυλίνδρου – Εύρεση ροπής αδράνειας.
Για τη μελέτη αυτή χρησιμοποιήσαμε το ακόλουθο βίντεο:
Εργαζόμαστε όπως προηγουμένως, οπότε προκύπτει η ανάλυση της εικόνας 10.
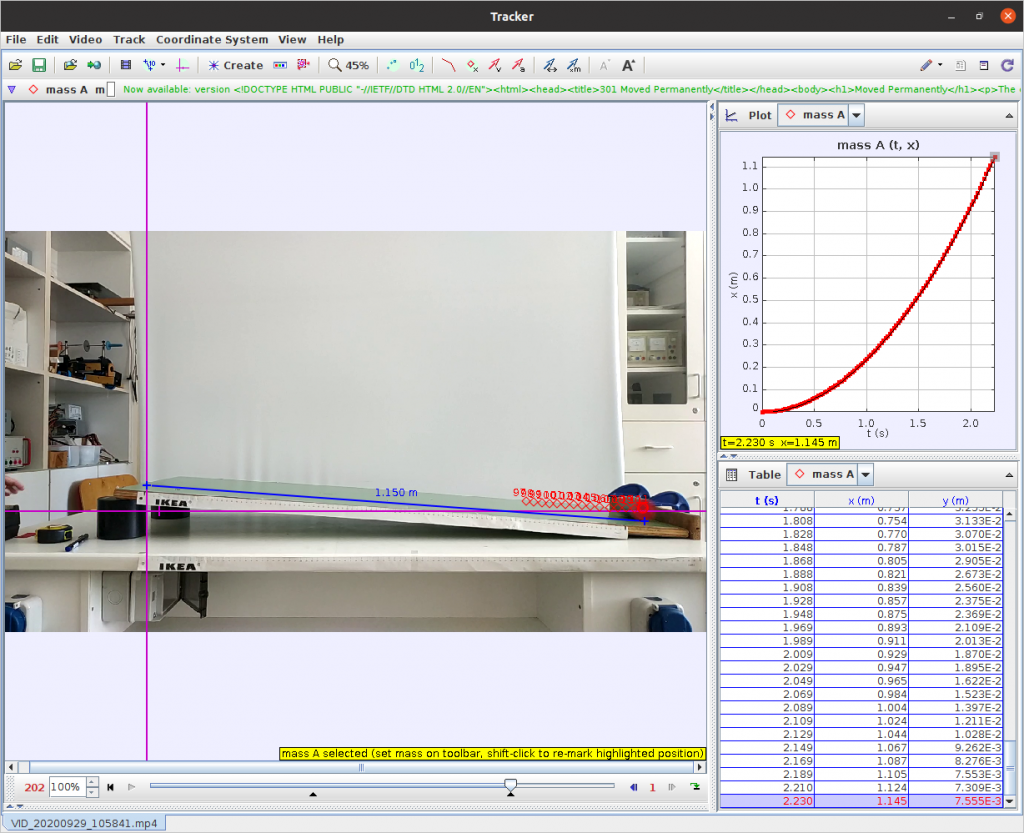
Εικόνα 10
Παρατηρείστε ότι το callibration stick είναι ουσιαστικά η ίδια η διαδρομή του κυλίνδρου, την οποία μετρήσαμε. Ο λόγος που επιλέχθηκε αυτή η απόσταση για πρότυπο μήκος και όχι, πχ, η ταινία που φαίνεται μπροστά από τη σανίδα, ήταν ότι στην περίπτωση της ταινίας και εξαιτίας της προοπτικής της γωνίας λήψης δημιουργούνται σφάλματα, τα οποία σε μία ποσοτική μελέτη ενός φαινομένου, μπορεί να αλλάξουν σημαντικά τις μετρήσεις.
Για την εύρεη της ροπής αδράνειας χρειαζόμαστε τη γωνία που σχηματίζει το κεκλιμένο επίπεδο με τον οριζόντιο άξονα. Επιλέγουμε το Create -> Measuring Tools -> Protractor (εικόνα 11).
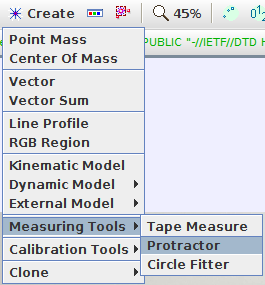
Εικόνα 11
Εμφανίζεται μία γωνία, τα άκρα και την κορυφή της οποίας μπορούμε σύρουμε, οπότε βρίσκουμε τη γωνία που θέλουμε (στην εικόνα 12 φαίνεται γωνία 4,2°).

Εικόνα 12
Στη συνέχεια, στο δεξιό μέρος της οθόνης και για τη “mass A” επιλέγουμε τη γραφική παράσταση “velocity magnitude” (συνισταμένη ταχύτητα), όπως φαίνεται στην εικόνα 13.
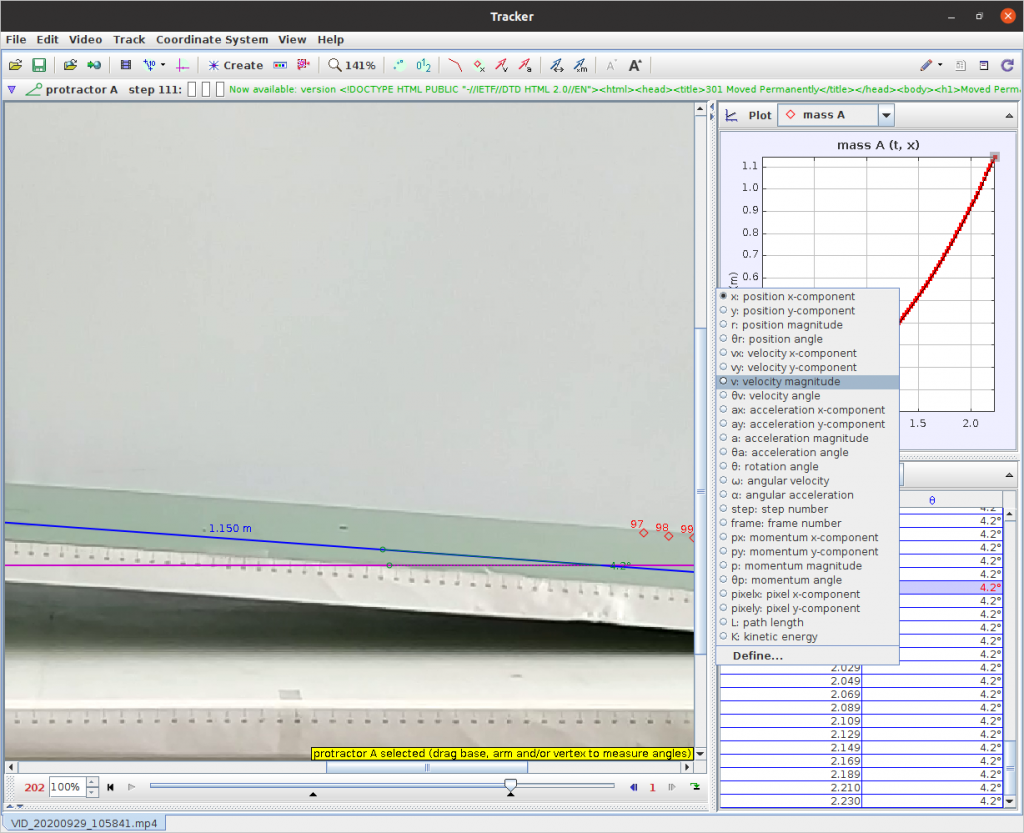
Εικόνα 13
Εμφανίζεται η γραφική παράσταση της εικόνας 14.
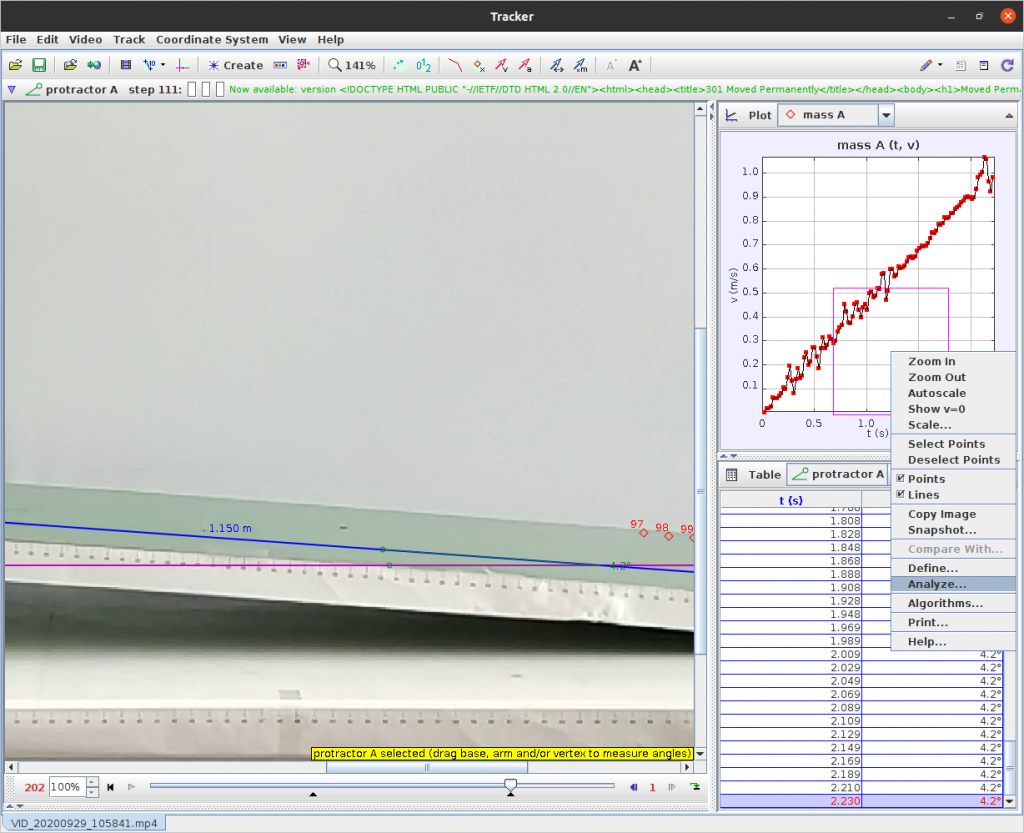
Εικόνα 14
Κάνοντας δεξί κλικ στη γραφική παράσταση και επιλέγοντας “Analyze”, προκύπτει η εικόνα 15.
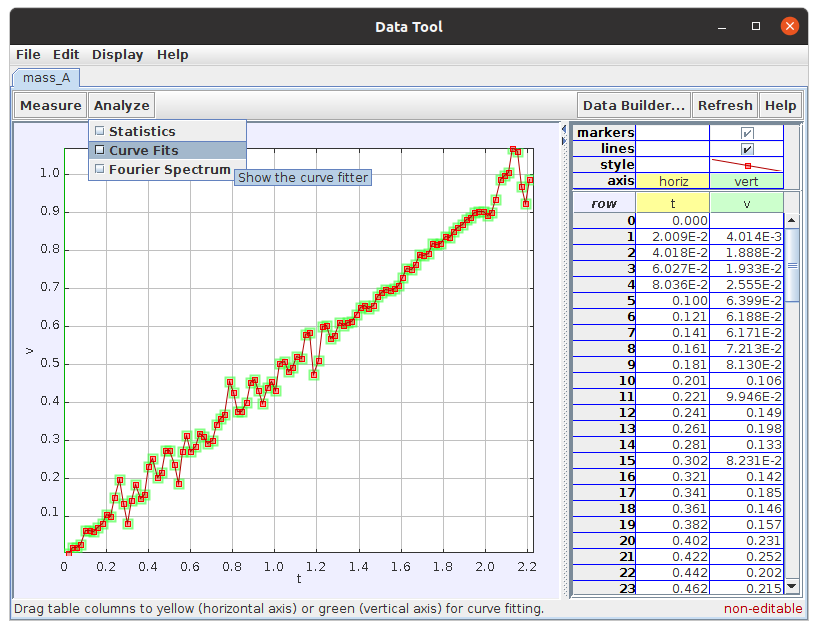
Εικόνα 15
Σε αυτό το παράθυρο, επιλέγοντας Analyze -> Curve Fits, παίρνουμε την εξίσωση της ευθείας που προκύπτει από τα δεδομένα μας. Η κλίση της ευθείας που προκύπτει είναι 0,45 (εικόνα 16), που αντιστοιχεί στη γραμμική επιτάχυνση του κυλίνδρου.
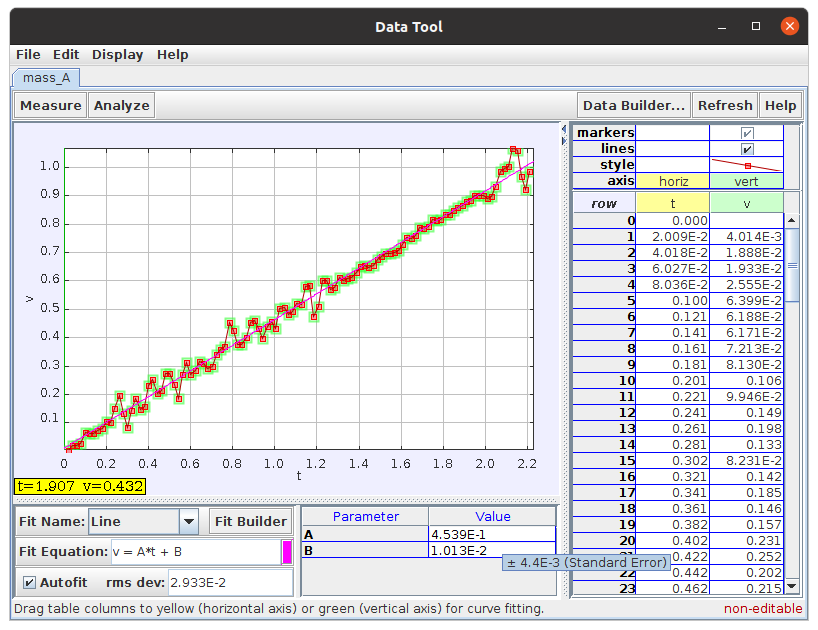
Εικόνα 16
Αν λάβουμε υπόψιν μας ότι η κύλιση οφείλεται στην τριβή, έχουμε
δηλαδή
και
όπου R=2,5 cm, θ=4,2°, α=0,4539 m/s2, g=9,81 m/s2, m=1 Kg και προκύπτει I=3,64 10-4 kg·m2.
Με βάση τη θεωρία, για κύλινδρο έχουμε
οπότε Ι=3,13 10-4 kg·m2.
